What is Decomposition Algorithm

Singular Value Decomposition Algorithms

Singular Value Decomposition concepts

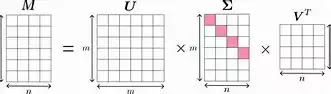
Singular Value Decomposition (SVD) is a matrix factorization technique used in various machine learning and data analysis applications. It decomposes a matrix into three separate matrices that capture the underlying structure of the original matrix. The three matrices that SVD produces are:

U: a unitary matrix that represents the left singular vectors of the original matrix.

S: a diagonal matrix that represents the singular values of the original matrix.

V: a unitary matrix that represents the right singular vectors of the original matrix.

Here is an example of how SVD works: Suppose we have a matrix that represents the ratings of users for different movies. We can use SVD to decompose this matrix into three separate matrices: one matrix that represents the preferences of users, one matrix that represents the importance of each movie, and one matrix that captures the relationship between users and movies.

matrix factorization technique used in various machine learning and data analysis applications

SVD can be used for various tasks, such as image compression, recommendation systems, and text analysis.

Singular Value Decomposition Algorithm

Define the problem and collect data.

Compute the matrix of user-item ratings.

Perform SVD on the matrix to obtain the matrices of left singular vectors, right singular vectors, and singular values.

Choose the number of latent factors to keep based on some criteria (e.g., explained variance).

Reconstruct the original matrix using the truncated SVD.

Predict the rating of a user for an item based on the reconstructed matrix.

Evaluate the model on a test dataset to estimate its performance.

Here is an example Python code for SVD using the Scikit-learn library:

python code

import numpy as np

from sklearn.decomposition import TruncatedSVD

# Create a sample matrix

matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])

# Apply SVD

svd = TruncatedSVD(n_components=2)

matrix_svd = svd.fit_transform(matrix)

# Print the decomposed matrices

print("Original matrix:\n", matrix)

print("U matrix:\n", svd.components_)

print("S matrix:\n", np.diag(svd.singular_values_))

print("V matrix:\n", matrix_svd)

Benefits of Singular Value Decomposition

It can reduce the dimensionality of large matrices, making it easier to analyze and manipulate them.

can determine a dataset's key characteristics.

It can improve the accuracy of prediction models by reducing noise and redundant information.

It can provide a compressed representation of the original matrix, which can be useful for storage and transmission.

Advantages of Singular Value Decomposition

Can handle sparse matrices and missing values.

Can work with non-linear and non-Gaussian Machine Learning Singular Value Decomposition

Can uncover latent factors that are not directly observable.

Disadvantages of Singular Value Decomposition

Costly to compute, especially for big datasets or complicated models.

is susceptible to noisy data and outliers.

It can be difficult to interpret the results of SVD, as the decomposed matrices may not have a clear interpretation.

Main Contents (TOPICS of Machine Learning Algorithms)
CONTINUE TO (Ensemble methods Algorithms)

Comments

Learn Machine Learning Algorithms

Machine Learning Algorithms with Python Code Contents of Algorithms 1. ML Linear regression A statistical analysis technique known as "linear regression" is used to simulate the relationship between a dependent variable and one or more independent variables. 2. ML Logistic regression Logistic regression: A statistical method used to analyse a dataset in which there are one or more independent variables that determine an outcome. It is used to model the probability of a certain outcome, typically binary (yes/no). 3. ML Decision trees Decision trees: A machine learning technique that uses a tree-like model of decisions and their possible consequences. It is used for classification and regression analysis, where the goal is to predict the value of a dependent variable based on the values of several independent variables. 4. ML Random forests Random forests: A machine learning technique that uses multiple decision trees to improve the accuracy of predictions. It creates a f

What is Linear regression

Linear regression A lgorithm Concept of Linear regression In order to model the relationship between a dependent variable and one or more independent variables, linear regression is a machine learning algorithm. The goal of linear regression is to find a linear equation that best describes the relationship between the variables. Using the values of the independent variables as a starting point, this equation can then be used to predict the value of the dependent variable. There is simply one independent variable and one dependent variable in basic linear regression. The linear equation takes the form of y = mx + b, where y is the dependent variable, x is the independent variable, m is the slope of the line, and b is the y-intercept. For example, let's say we have a dataset of the number of hours studied and the corresponding test scores of a group of students. We can use linear regression to find the relationship between the two variables and predict a student's test scor

What is Logistic regression

Logistic Regression Algorithm Concept of Logistic Regression A machine learning approach called logistic regression is used to model the likelihood of a binary outcome based on one or more independent factors. The goal of logistic regression is to find the best-fitting logistic function that maps the input variables to a probability output between 0 and 1. The logistic function, also known as the sigmoid function, takes the form of: sigmoid(z) = 1 / (1 + e^-z) where z is a linear combination of the input variables and their coefficients. For example, let's say we have a dataset of customer information, including their age and whether they have purchased a product. We can use logistic regression to predict the probability of a customer making a purchase based on their age. Logistic Regression Algorithm: Define the problem and collect data. Choose a hypothesis class (e.g., logistic regression). Define a cost function to measure the difference between predicted and actual

What is Naive Bayes algorithm

Naive Bayes Algorithm with Python Concepts of Naive Bayes Naive Bayes is a classification algorithm based on Bayes' theorem, which states that the probability of a hypothesis is updated by considering new evidence. Since it presumes that all features are independent of one another, which may not always be the case in real-world datasets, it is known as a "naive". Despite this limitation, Naive Bayes is widely used in text classification, spam filtering, and sentiment analysis. Naive Bayes Algorithm Define the problem and collect data. Choose a hypothesis class (e.g., Naive Bayes). Compute the prior probability and likelihood of each class based on the training data. Use Bayes' theorem to compute the posterior probability of each class given the input features. Classify the input by choosing the class with the highest posterior probability. Evaluate the model on a test dataset to estimate its performance. Here's an example code in Python for Naive Bayes: Python cod

Search This Blog