Skip to main content

What is Principal Component Analysis

Principal Component Analysis Algorithm

Principal Component Analysis Concept

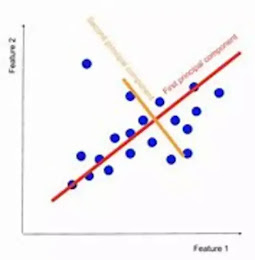
Principal Component Analysis (PCA) is a dimensionality reduction technique used to transform high-dimensional datasets into a lower-dimensional space while preserving as much of the variance as possible. It works by identifying the principal components that capture the most significant variation in the data and projecting the data onto these components.

Suppose we have a dataset of images with 1000 pixels each. We want to reduce the dimensionality of the dataset to 100 pixels to reduce the computational complexity. We use PCA to identify the principal components that capture the most significant variation in the images. We project the images onto these components to obtain a lower-dimensional representation of the images.

reduction technique used to transform high-dimensional datasets into a lower-dimensional datasets

Principal Component Analysis Algorithm

  • Define the problem and collect data.
  • Compute the covariance matrix of the data.
  • Compute the eigenvectors and eigenvalues of the covariance matrix.
  • Choose the top k eigenvectors with the largest eigenvalues.
  • Transform the data into the new k-dimensional space defined by the eigenvectors.
  • Evaluate the model on a test dataset to estimate its performance.

Here is a sample Python code for the PCA algorithm using the sci-kit-learn library:

python code

from sklearn.datasets import load_iris

from sklearn.decomposition import PCA

import matplotlib.pyplot as plt

# Load the iris dataset

iris = load_iris()

# Create a PCA object

pca = PCA(n_components=2)

# Fit and transform the data

X_pca = pca.fit_transform(iris.data)

# Plot the data in the new 2D space

plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target)

plt.label('PCA Component 1')

plt.label('PCA Component 2')

plt.show()

PCA algorithm using the sci-kit-learn

Advantages of PCA Algorithm:

  • The algorithm is computationally efficient.
  • The algorithm is simple to implement.
  • The algorithm is resistant to anomalies and noise.
  • The algorithm can handle missing values.

Disadvantages of the PCA Algorithm:

  • It could be challenging to interpret the primary components.
  • The choice of the number of principal components can be subjective.
  • The algorithm may not work well for non-linearly separable data.
  • The algorithm may not be suitable for datasets with categorical variables.

Main Contents (TOPICS of Machine Learning Algorithms) 
                                  CONTINUE TO (K-Means clustering algorithm)

Labels:
Location: Guntur, Andhra Pradesh, India

Comments

Post a Comment

Popular posts from this blog

Learn Machine Learning Algorithms

Machine Learning Algorithms with Python Code Contents of Algorithms  1.  ML Linear regression A statistical analysis technique known as "linear regression" is used to simulate the relationship between a dependent variable and one or more independent variables. 2.  ML Logistic regression  Logistic regression: A statistical method used to analyse a dataset in which there are one or more independent variables that determine an outcome. It is used to model the probability of a certain outcome, typically binary (yes/no). 3.  ML Decision trees Decision trees: A machine learning technique that uses a tree-like model of decisions and their possible consequences. It is used for classification and regression analysis, where the goal is to predict the value of a dependent variable based on the values of several independent variables. 4.  ML Random forests Random forests: A machine learning technique that uses multiple decision trees to improve the accuracy of predicti...
Post a Comment
Read more

What is Naive Bayes algorithm

Naive Bayes Algorithm with Python Concepts of Naive Bayes Naive Bayes is a classification algorithm based on Bayes' theorem, which states that the probability of a hypothesis is updated by considering new evidence. Since it presumes that all features are independent of one another, which may not always be the case in real-world datasets, it is known as a "naive". Despite this limitation, Naive Bayes is widely used in text classification, spam filtering, and sentiment analysis. Naive Bayes Algorithm Define the problem and collect data. Choose a hypothesis class (e.g., Naive Bayes). Compute the prior probability and likelihood of each class based on the training data. Use Bayes' theorem to compute the posterior probability of each class given the input features. Classify the input by choosing the class with the highest posterior probability. Evaluate the model on a test dataset to estimate its performance. Here's an example code in Python for Naive Bayes: Python cod...
Post a Comment
Read more

What is Linear regression

Linear regression A lgorithm Concept of Linear regression In order to model the relationship between a dependent variable and one or more independent variables, linear regression is a machine learning algorithm. The goal of linear regression is to find a linear equation that best describes the relationship between the variables. Using the values of the independent variables as a starting point, this equation can then be used to predict the value of the dependent variable. There is simply one independent variable and one dependent variable in basic linear regression. The linear equation takes the form of y = mx + b, where y is the dependent variable, x is the independent variable, m is the slope of the line, and b is the y-intercept. For example, let's say we have a dataset of the number of hours studied and the corresponding test scores of a group of students. We can use linear regression to find the relationship between the two variables and predict a student's test scor...
Post a Comment
Read more

What is Logistic regression

Logistic Regression  Algorithm Concept of Logistic Regression A machine learning approach called logistic regression is used to model the likelihood of a binary outcome based on one or more independent factors. The goal of logistic regression is to find the best-fitting logistic function that maps the input variables to a probability output between 0 and 1. The logistic function, also known as the sigmoid function, takes the form of:   sigmoid(z) = 1 / (1 + e^-z)   where z is a linear combination of the input variables and their coefficients. For example, let's say we have a dataset of customer information, including their age and whether they have purchased a product. We can use logistic regression to predict the probability of a customer making a purchase based on their age. Logistic Regression  Algorithm: Define the problem and collect data. Choose a hypothesis class (e.g., logistic regression). Define a cost function to measure the difference between predic...
Post a Comment
Read more

What is Convolutional and Recurrent Neural Networks

Convolutional Neural Networks and Recurrent  Neural Networks Algorithms Convolutional NN - Recurrent NN Concepts Neural networks, including deep learning architectures such as Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs) The machine learning technique known as neural networks was inspired by the design and function of the human brain. They consist of interconnected nodes, or "neurons", that process and transmit information to each other to make a prediction or decision. Deep learning architectures such as Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs) are advanced neural network structures that have proven to be highly effective in a variety of applications including time series analysis, natural language processing, and picture and audio recognition. Convolutional Neural Networks (CNNs) are a type of neural network that is designed to process and analyze image data. They use convolutional layers, which apply ...
Post a Comment
Read more